Insider Brief
- DeepSeek-AI researchers propose a new neural network architecture that allows models to scale with wider internal connections while maintaining stable training behavior.
- The approach constrains how information is mixed between layers, preventing signals and gradients from exploding or vanishing in large models.
- Large-scale experiments show the design improves performance and stability with only modest additional training overhead.
A study by a team of researchers at DeepSeek-AI proposes a new way to expand the internal connections of large neural networks while preserving training stability, addressing a growing bottleneck in how today’s largest language models are built and scaled.
“To address these challenges, we propose Manifold-Constrained Hyper-Connections (mHC), a general framework that projects the residual connection space of HC onto a specific manifold to restore the identity mapping property, while incorporating rigorous infrastructure optimization to ensure efficiency,” the researchers write.
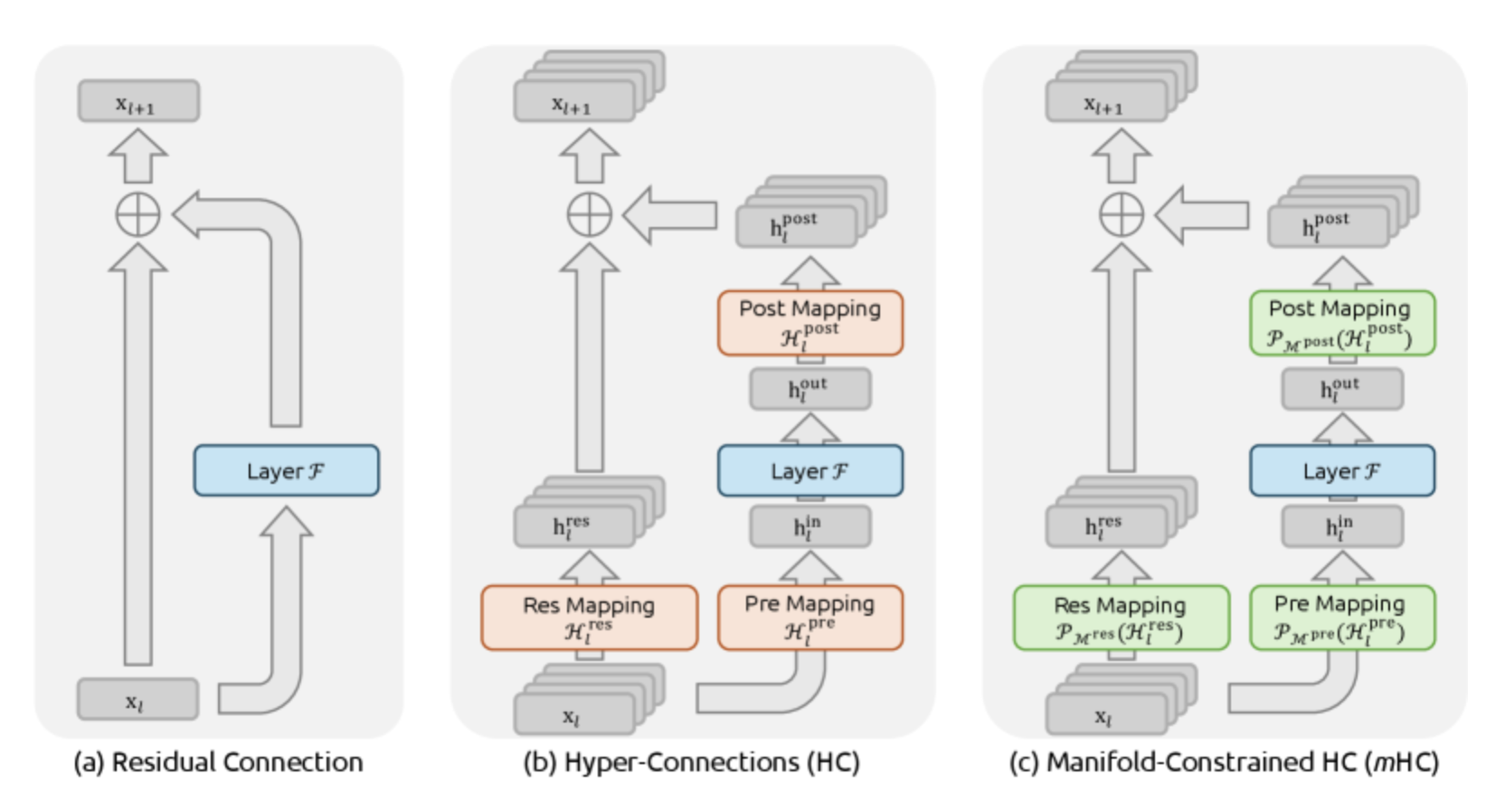
This architectural framework modifies how information flows between layers in deep neural networks. The approach aims to retain the performance benefits of wider and more flexible connections while restoring a core property that has made residual networks trainable at massive scale for more than a decade.
At stake is the reliability of training increasingly large models. As architectures become more complex, small design choices in how layers connect can lead to runaway numerical behavior, stalled training runs, or excessive system overhead. The study argues that these issues are not incidental but structural—and that they can be fixed with mathematical constraints rather than trial-and-error tuning.
Why Residual Connections Matter
Modern deep learning relies heavily on residual connections, a design first popularized in computer vision and later embedded into Transformer-based language models. In simple terms, residual connections allow each layer to pass its input forward unchanged, alongside whatever new transformation the layer computes. This identity path helps signals and gradients move through hundreds of layers without fading away or blowing up.
Recent work on Hyper-Connections sought to improve performance by widening this residual pathway. Instead of a single stream of features flowing through the network, Hyper-Connections create multiple parallel streams that mix information across layers. This added flexibility has been shown to improve accuracy on language tasks without increasing the core computation of each layer.
But the DeepSeek-AI researchers show that this added freedom comes at a cost. In standard residual connections, the identity mapping ensures that the average strength of signals remains stable as they propagate. In Hyper-Connections, that guarantee disappears. Because the mixing matrices between streams are unconstrained, small deviations compound across layers, causing signals to grow uncontrollably or shrink toward zero.
The study documents this effect in large-scale training runs, where models using unconstrained Hyper-Connections exhibit sudden loss spikes and unstable gradients. These failures emerge not from optimization settings or data issues, but from the architecture itself.
Restoring Stability
The central idea behind mHC is to restrict how residual streams are mixed, but without eliminating mixing altogether. The researchers do this by constraining the residual connection matrices to live on a specific mathematical object known as the Birkhoff polytope, which consists of doubly stochastic matrices.
In practical terms, a doubly stochastic matrix has nonnegative entries and rows and columns that each sum to one. This ensures that each output stream is a weighted average of the inputs rather than an amplification or cancellation. As a result, the overall signal strength is preserved.
The study shows that this constraint restores three properties critical to stable training. First, the transformation does not increase the size of signals or gradients. Second, stacking many such layers together preserves this behavior across the entire depth of the network. Third, the constrained matrices still allow meaningful information mixing, acting as smooth combinations of permutations rather than rigid identity paths.
To enforce these constraints during training, the researchers use an iterative normalization procedure that projects each residual mapping onto the allowed manifold. While the underlying mathematics is complex, the operational effect is straightforward: the network is prevented from learning unstable shortcuts while retaining flexibility.
DeepSeek-AI researchers report that when the expansion factor collapses to one stream, the method reduces exactly to a standard residual connection, showing that mHC generalizes rather than replaces existing designs.
Potential Performance Gains
Beyond numerical stability, the study addresses a second problem with wider residual streams: memory and communication overhead. Expanding the residual pathway multiplies the amount of data that must be moved between GPUs and stored for backpropagation, often becoming a dominant bottleneck.
The researchers describe a set of infrastructure optimizations that make mHC practical at scale. These include fusing multiple operations into single GPU kernels, recomputing intermediate values during backpropagation instead of storing them, and overlapping communication with computation in pipeline-parallel training setups.
In large language model experiments ranging from billions to tens of billions of parameters, models using mHC trained stably and consistently outperformed both standard architectures and unconstrained Hyper-Connections on downstream benchmarks. The reported training-time overhead was modest, on the order of a single-digit percentage increase even with four parallel residual streams.
Scaling experiments showed that the performance advantage persisted as model size and training compute increased, suggesting that the approach does not degrade at larger scales. Stability analyses further demonstrated that signal amplification was reduced by orders of magnitude compared with unconstrained designs.
The study positions mHC as a framework rather than a single fixed solution. While it focuses on doubly stochastic constraints, the team indicates that other geometric constraints could be explored to balance flexibility and stability in different ways.
More broadly, the work revives attention on macro-architecture — the global structure of how layers connect — at a time when most innovation has focused on layer internals or scaling laws. As models grow larger and more expensive to train, architectural stability becomes a first-order concern rather than an implementation detail.
Ultimately, the researchers hope that by showing that training failures can arise from subtle violations of identity mapping — and that these failures can be prevented with principled constraints — their study offers a path toward more reliable large-scale model design.
If adopted widely, such approaches could reduce wasted compute, improve reproducibility, and open new directions for scaling neural networks beyond current limits.
“We anticipate that mHC, as a flexible and practical extension of HC, will contribute to a deeper understanding of topological architecture design and suggest promising directions for the evolution of foundational models,” the team writes.